- Lambda = 0.0129. This value is close to the present value.
- Lambda = 0.06
- Lambda = 0. In this case two different C parameters are considered:
- C = 60
- C = 2
-
Lambda = 0.0129 C = 60 k = 0
H0 = 69,992 1/H0 = 13,999 Omega(Lambda)=0,73745 
Picture 1A H0 = 66,778 1/H0 = 14,673 Omega(Lambda)=0,81013 
Picture 2A H0 = 63,211 1/H0 = 15,501 Omega(Lambda)=0,90413 
Picture 3A 
Picture 1B age=14 Picture 2B age=16 Picture 3B age=20 -
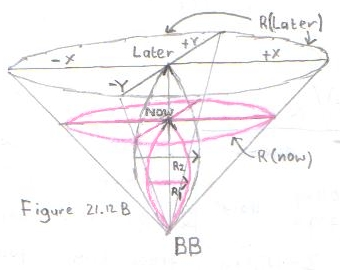
The top three pictures above show the size of the Universe in the x direction with Lambda = 0.01129 when the parameter age has the values: 14 16 and 20.
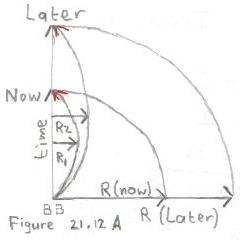
- The black line. This line shows the size of the Universe. This is the maximum distance from which something can be observed.
- The pink line, This line shows events at 1/5 of the radius of the Universe.
- The blue line. This line shows the path of a light ray which started as close as possible near the Big Bang and which reaches the Observer at present.
- The green line. This line shows the path of a light ray which started at the pink line 2 billion years after the Big Bang.
The bottom three pictures above show the detail for the first 1 billion years.
Picture 1A shows the situation where H0=70 Mpc, 1/H0=14 Omega m=0.262 and omega L=0,737 which are the values close to what is presently measured or calculated.
The most important lines are:
The area below the blue line identify events which reached the observer in the past.When you compare the three smaller pictures you will see that the starting events moved towards the right. They happened respectively 300000, 500000 and 700000 years after the Big Bang. The Black line in all the three pictures means the same.
Picture 3B shows all the events starting 700000 years after the Big Bang until present which is 20 Billion years after the Big Bang.
Picture 2B shows all the events starting 500000 years after the Big Bang until present which is 16 Billion years after the Big Bang.
Compare picture 3B with picture 2B than the events between 500000 years and 700000 years disappeared but new events between 16 billion years and 20 billion years appeared.
The galaxies between 1 billion years and 16 billion years (which are visible on both) aged.In short, in total: you can observe more
H0 = 61,324 Omega(Lambda)=0,96065 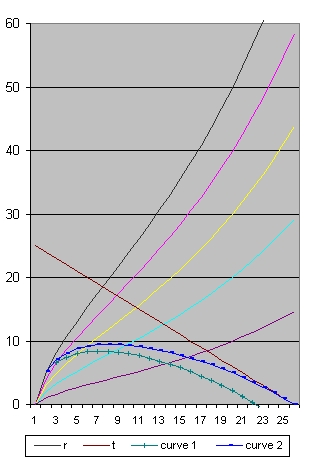
Picture 4 age=25 H0 = 60,588 Omega(Lambda)=0,98413 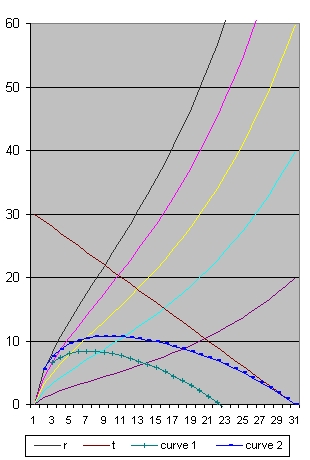
Picture 5 age=30 H0 = 60,182 Omega(Lambda)=0,99746 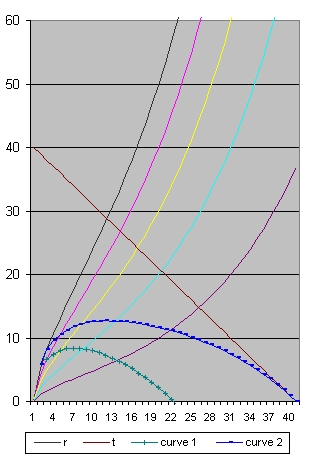
Picture 6 age=40 -
To study this aging in more detail go back to Picture 1A
- In Picture 1A the Blue line starts at the Pink line. It is the Pink line which we will follow. The Pink line represents the path of a galaxy. In this galaxy we observe for example a super nova
In Picture 1A this super nova happens after 1 billion years at a distance from roughly 4 billion light years. - In Picture 2A we study the point where the blue line crosses the pink line. This is after roughly 1.4 billion years at a distance from 5 billion light years.
- In picture 3A the point where the two lines cross is after roughly 2 billion years at a distance from 7 billion light years.
- In picture 4 the point is at 2.5 billion years at a distance from 8 billion light years
- In picture 5 the point is at 3 billion years at a distance from 9 billion light years
- In picture 6 the point is at 4 billion years at a distance from 10.5 billion light years
-
Lambda = 0.06 C = 60 k = 0
The corresponding pictures below have the same age, but Lambda is different.
When you study the pictures 7B, 8B and 9B the starting events are 150000, 200000 and 250000 years after the Big Bang. This means almost nothing disappears from view and almost only new events appear.
What is also important that the point where the blue line crosses the pink line, happened 1 billion years after the Big Bang at a distance of 4 billion light years. This point almost does not move. There is no aging.-
The behaviour of the green line for Lambda=0.06 is rather spectacular compared with Lambda=0.01129
- With Lambda=0.06 this specific event is not observed. In that case the green line does not cross the horizontal time line. The reason is acceleration.
- With Lambda=0.0129 this specific event is observed. That is the moment when the green line crosses the horizontal time axis. This is after roughly 22 billion years.
H0 = 139,2804 Omega(Lambda)=0,98953 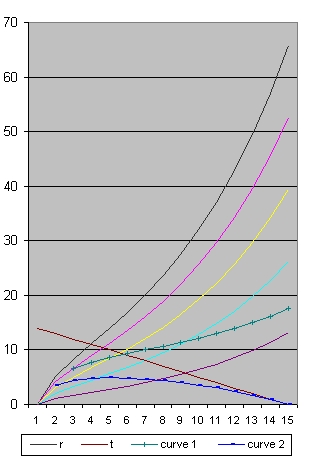
Picture 7A H0 = 138,8619 Omega(Lambda)=0,99551 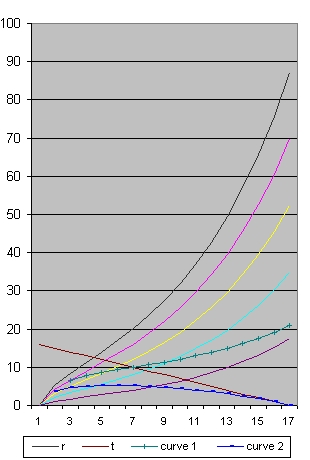
Picture 8A H0 = 138,6068 Omega(Lambda)=0,99918 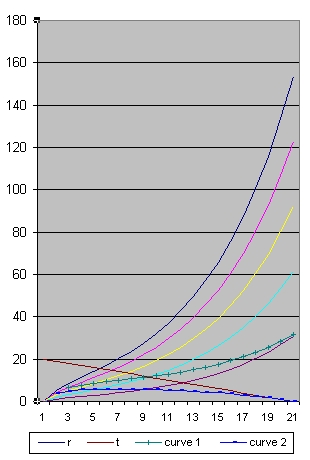
Picture 9A 
Picture 7B age=14 Picture 8B age=16 Picture 9B age=20 H0 = 138,5565 Omega(Lambda)=0,99990 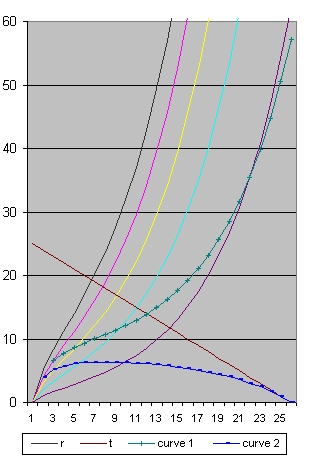
Picture 10 age=25 H0 = 138,5505 Omega(Lambda)=0,99999 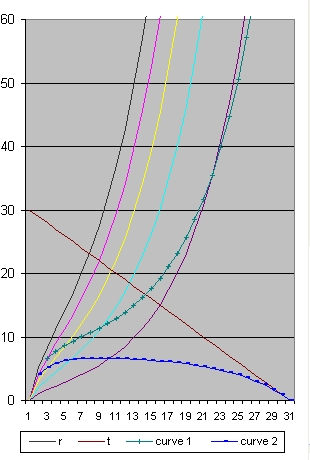
Picture 11 age=30 H0 = 138,5497 Omega(Lambda)=1 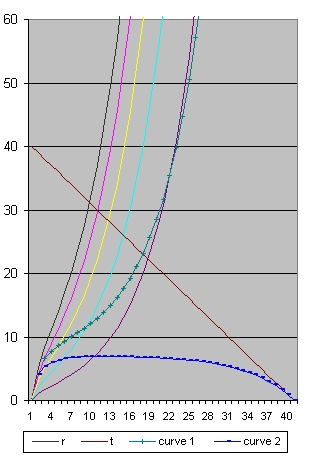
Picture 12 age=40 -
Lambda = 0
-
With Lambda is zero two different values of C are considered.
- With C = 60. This is the same value as discussed above
- With C = 2
C = 60
-
When you compare the figures among each other you will see
- In picture 13 (age 14 Year) the oldest galaxies you can observe is roughly 0.5 years after the Big Bang.
- In picture 14 (age 20 Year) the oldest galaxies you can observe is roughly 1 years after the Big Bang.
- In picture 15 (age 40 Year) the oldest galaxies you can observe is roughly 4.5 years after the Big Bang.
-
You can also compare Picture 13 with Picture 1A (Both age 14 b years) and Picture 15 with Picture 6 (Both age 40 b years)
and study the influence of the parameter Lambda.
- In picture 1A (age 14 Year) the oldest galaxies you can observe is roughly 0.5 years after the Big Bang.
- In picture 6 (age 40 Year) the oldest galaxies you can observe is roughly 2 years after the Big Bang.
When you compare Picture 15 with Picture 6 this result is even more pronounced.
H0 = 46,646 Omega(Lambda) = 0 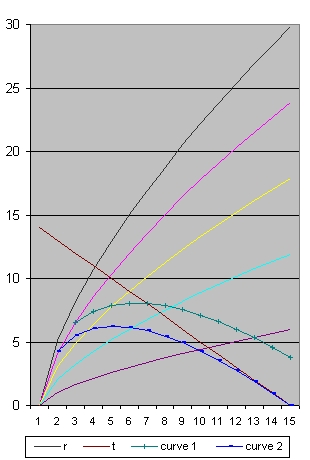
Picture 13 age=14 H0 = 32,665 Omega(Lambda) = 0 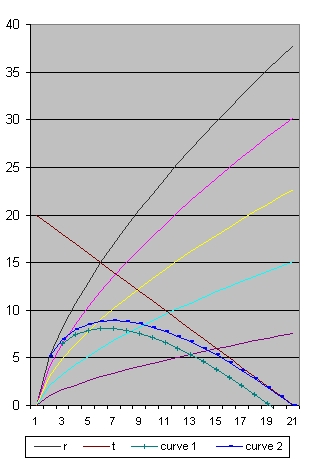
Picture 14 age=20 H0 = 16,329 Omega(Lambda) = 0 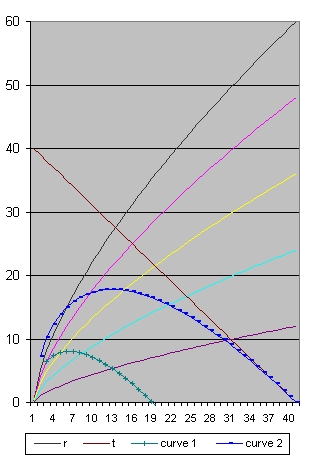
Picture 15 age=40 C = 2
-
When you compare the figures among each other you will see
- In picture 16 (age 14 Year) the oldest galaxies you can observe is roughly 6.5 years after the Big Bang.
- In picture 17 (age 20 Year) the oldest galaxies you can observe is roughly 10 years after the Big Bang.
- In picture 18 (age 40 Year) the oldest galaxies you can observe is roughly 23 years after the Big Bang.
-
You can also compare C = 2 with C = 60
In that case the galaxies you can see are the same but the age in C=2 is older.
H0 = 46,654 Omega(Lambda) = 0 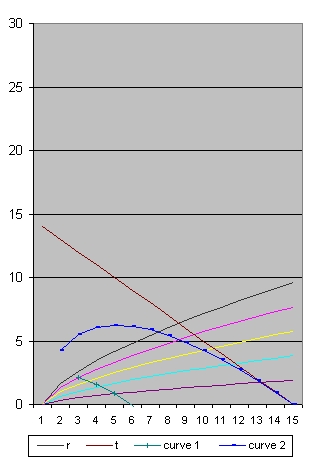
Picture 16 age=14 H0 = 32,659 Omega(Lambda) = 0 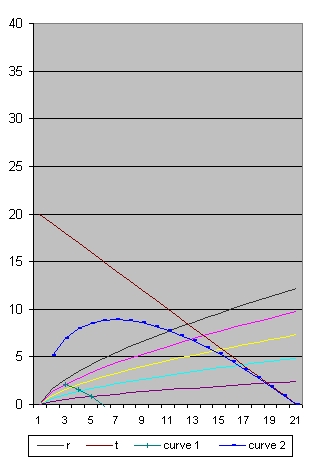
Picture 17 age=20 H0 = 16,330 Omega(Lambda) = 0 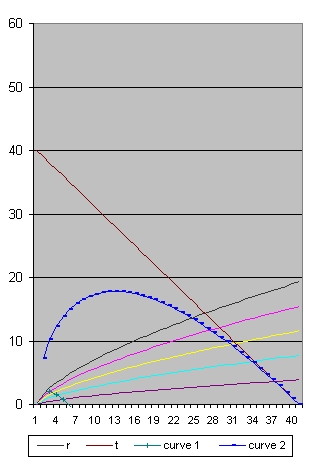
Picture 18 age=40
|
Consider a sphere in space with a fixed radius. As a consequence of space expansion the number of galaxies within that sphere will diminish. When space expansion is accelerating this number will even decrease even faster. This is a density problem and is important for the local region of the Universe surrounding us. What we are discussing here is the age of the youngest galaxies we can observe. Generally speaking the age of the youngest galaxies will slowly increase but the total number of galaxies we can see will stay the same assuming our own galaxy will still exist. A second complexity is a Luminosity problem. The Luminosity problem has to do how long we can observe the youngest galaxy. This has nothing to do with the present position of the galaxy nor if space expansion is accelerating. The Luminosity problem is a function of the light travel time i.e the distance between the present time and the age of the youngest star. As a result the light received will be dimmer and the galaxy will become invisible assuming we use the same equipment. In short: the total number of galaxies observed on the long run will decrease |
To read more about the pictures see: Friedmann's equation & the path of a light ray 13 Questions
2. Cosmography of the Local Universe
For the most current image of the positions of the galaxies see this: 3-D map of Universe shows galaxies in unprecedented detail The video is brilliant, is an eye catcher and gives a good impression about the current state of science and astronomy.It should be mentioned that the distances involved are "small" relative to the total size of the Universe.